Найти пересечение массивов

Пересечение массивов — это одна из самых распространенных задач, с которыми сталкиваются разработчики при работе с большими объемами данных. Независимо от того, в каких целях вы используете массивы — для анализа данных, построения графиков или реализации алгоритмов машинного обучения — поиск общих элементов является неотъемлемой частью этого процесса.

Однако, эффективный поиск пересечения массивов может быть сложной задачей, особенно при работе с массивами большого размера. Существует несколько методов решения этой задачи, которые имеют свои преимущества и недостатки в зависимости от размера и характеристик массивов.

Один из наиболее популярных методов — использование хэш-таблицы или множества для хранения элементов одного из массивов, а затем перебор всех элементов другого массива и проверка наличия каждого элемента в хэш-таблице. Такой подход позволяет найти пересечение массивов за линейное время, что является очень быстрой операцией, особенно при работе с большими объемами данных.

Еще одним эффективным методом является сортировка обоих массивов и последующий проход по ним с использованием двух указателей. Этот метод также позволяет найти пересечение массивов за линейное время, но требует предварительной сортировки массивов, что может занимать дополнительное время, особенно при работе с массивами большого размера.

Понятие пересечения массивов

Для выполнения задачи по поиску пересечения массивов существуют различные эффективные методы. Один из наиболее популярных способов — это использование хэш-таблицы для отслеживания уникальных элементов в каждом массиве и нахождения общих элементов.

Шаги поиска пересечения массивов с использованием хэш-таблицы:

Создайте пустую хэш-таблицу.
Пройдитесь по каждому элементу первого массива и добавьте его в хэш-таблицу.
Пройдитесь по каждому элементу второго массива и проверьте, есть ли он в хэш-таблице. Если есть, добавьте его в новый массив пересечения.
Повторяйте шаги 3-4 для каждого следующего массива, пока не пройдете все исходные массивы.

Использование хэш-таблицы позволяет значительно ускорить поиск пересечения массивов, так как проверка наличия элемента в хэш-таблице выполняется за константное время (O(1)). Кроме того, этот метод гарантирует, что элементы в новом массиве пересечения будут уникальными.

Однако стоит отметить, что этот метод имеет ограничение на размер памяти, так как необходимо создать хэш-таблицу, которая может занимать значительное количество памяти при больших исходных массивах. Поэтому, при выборе метода поиска пересечения массивов, необходимо учитывать и объем данных, с которыми будет работать алгоритм.

В итоге, понятие пересечения массивов включает в себя операцию нахождения общих элементов между двумя или более массивами с использованием различных методов, таких как использование хэш-таблицы. Эта операция может быть полезна во многих случаях, например, для нахождения общих элементов в сравнительных исследованиях, определения пересечений в множествах данных или фильтрации дубликатов.

Определение и особенности

Пересечение массивов представляет собой операцию поиска общих элементов между двумя или более массивами. Это полезный инструмент при работе с данными, особенно в задачах анализа и обработки больших объемов информации.

Операция пересечения

Операция пересечения массивов заключается в нахождении элементов, которые присутствуют одновременно в двух или более массивах. Результатом пересечения является новый массив, содержащий только эти общие элементы.

Определение пересечения массивов может быть различным в зависимости от контекста. Например, пересечение может быть определено как множество значений, которые присутствуют во всех заданных массивах. Или пересечение может быть определено как массив, содержащий только уникальные элементы, которые присутствуют во всех массивах один раз.

Эффективные методы поиска пересечения

Существует несколько эффективных методов поиска пересечения, которые могут быть применены в различных ситуациях:

Метод с использованием хэш-таблицы: в этом методе каждый элемент массива добавляется в хэш-таблицу. Затем происходит проверка каждого элемента второго массива на наличие в хэш-таблице, и если элемент присутствует, он добавляется в результирующий массив.
Метод с использованием сортировки и двоичного поиска: в этом методе массивы сортируются, затем для каждого элемента одного массива выполняется двоичный поиск во втором массиве. Если элемент найден, он добавляется в результирующий массив.
Метод с использованием битовых операций: в этом методе каждый элемент массива представляется в виде битового числа, а затем производятся операции И или ИЛИ над битовыми числами, чтобы найти общие элементы.

Выбор метода зависит от размера и типа данных в массивах, а также от требуемой скорости и потребления памяти. Каждый метод имеет свои преимущества и ограничения, и подходящий метод выбирается в зависимости от конкретных условий задачи.

Распространенные способы поиска пересечения массивов

Найти пересечение массивов может быть важной задачей при работе с данными. Это означает найти элементы, которые есть в обоих массивах. Существует несколько эффективных способов, которые позволяют достичь данного результата.

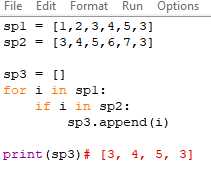
1. Использование цикла: одним из простейших способов поиска пересечения массивов является использование цикла. При этом мы сравниваем каждый элемент первого массива с каждым элементом второго массива. Если элементы совпадают, то добавляем его в результирующий массив. В итоге получаем массив, содержащий общие элементы.

2. Использование метода filter(): с помощью метода filter() можно получить новый массив, содержащий только те элементы, которые удовлетворяют определенному условию. Для поиска пересечения двух массивов можно использовать этот метод, указав условие сравнения элементов.

3. Использование метода includes(): метод includes() позволяет проверить, содержит ли массив определенный элемент. Можно использовать этот метод для проверки каждого элемента первого массива на наличие во втором массиве. Если элемент содержится во втором массиве, то добавляем его в результирующий массив.

4. Использование метода Set: структура данных Set позволяет хранить набор уникальных элементов. При создании Set из первого массива, а затем применении метода filter() или forEach() к этому Set, можно получить массив, содержащий только те элементы, которые есть и в первом, и во втором массиве.

5. Использование метода reduce(): метод reduce() позволяет применить функцию к элементам массива и построить один результирующий элемент. Для поиска пересечения двух массивов можно использовать метод reduce(), применяя операцию поиска общих элементов к каждому элементу первого массива и аккумулируя результат.

Выбор подходящего способа поиска пересечения массивов зависит от контекста и требований задачи. Важно учитывать эффективность и удобство использования каждого метода. Используя эти распространенные способы, вы сможете эффективно находить общие элементы в массивах и решать свои задачи.

Перебор элементов вложенными циклами

Идея заключается в том, что мы используем два цикла: внешний цикл, который перебирает элементы одного массива, и внутренний цикл, который перебирает элементы другого массива. На каждой итерации внутреннего цикла мы сравниваем текущие элементы и проверяем, совпадают ли они. Если да, то мы добавляем этот элемент в результирующий массив или выполняем нужные действия.

Однако следует отметить, что этот метод имеет высокую сложность времени выполнения O(n^2), где n — это суммарное количество элементов в обоих массивах. Это означает, что время выполнения будет расти быстро с увеличением размера массивов. Если массивы очень большие, этот метод может стать неэффективным и привести к замедлению работы программы.

Тем не менее, перебор элементов вложенными циклами может быть полезным для небольших массивов или в случаях, когда точность и простота реализации имеют большее значение, чем производительность. Кроме того, этот метод можно комбинировать с другими методами для более точного и эффективного решения задачи.

Сортировка массивов и два указателя

Идея заключается в том, что если оба массива отсортированы по возрастанию, то элементы, которые присутствуют одновременно в обоих массивах, будут находиться рядом друг с другом.

Для этого можно использовать два указателя — один для первого массива и один для второго массива. Начиная с начала обоих массивов, мы двигаем указатели вправо или влево, в зависимости от того, какой элемент меньше.

Когда указатели указывают на одинаковые элементы, мы добавляем этот элемент в результирующий массив общих элементов.

Такой подход позволяет нам эффективно найти пересечение массивов, так как мы используем сортировку, чтобы снизить время поиска общих элементов.

Примером реализации этого подхода может быть следующий код:

 function findIntersection(arr1, arr2) { arr1.sort(); arr2.sort(); let intersection = []; let i = 0; let j = 0; while (i < arr1.length && j < arr2.length) { if (arr1[i] < arr2[j]) { i++; } else if (arr1[i] > arr2[j]) { j++; } else { intersection.push(arr1[i]); i++; j++; } } return intersection; }

Использование хеш-таблицы

Алгоритм работы с хеш-таблицей следующий:

Создается пустая хеш-таблица.
Проходя по первому массиву, каждый элемент добавляется в хеш-таблицу как ключ.
Проходя по второму массиву, проверяется наличие каждого элемента в хеш-таблице. Если элемент уже присутствует, то он добавляется в результирующий массив.

Такой подход позволяет быстро находить общие элементы за время, пропорциональное сумме длин обоих массивов. Потребность в поиске каждого элемента в хеш-таблице занимает константное время, что делает этот алгоритм очень эффективным.

Однако, стоит учитывать, что использование хеш-таблицы требует дополнительных затрат по памяти для хранения самой таблицы. Также, при коллизиях (ситуация, когда два элемента имеют одинаковый хеш-код) требуется дополнительная обработка, чтобы избежать потери данных.

Использование стандартных методов языка

Современные языки программирования часто предоставляют встроенные методы для работы с массивами, включая поиск пересечений. Использование стандартных методов языка может быть эффективным способом найти общие элементы в массивах.

Одним из наиболее распространенных методов является использование метода intersection() для списков или множеств в языках, таких как Python или Java. Этот метод позволяет получить пересечение двух массивов без необходимости реализации алгоритма поиска пересечений вручную.

В Python, например, можно использовать встроенную функцию intersection() модуля set для нахождения пересечения двух списков:

 list1 = [1, 2, 3, 4, 5] list2 = [4, 5, 6, 7, 8] intersection = list(set(list1).intersection(list2)) print(intersection)

Результат выполнения кода будет содержать только общие элементы из двух исходных списков: [4, 5].

Аналогичным образом в Java можно использовать класс java.util.Set и его метод retainAll() для нахождения пересечения двух множеств:

 import java.util.HashSet; import java.util.Set; public class Main { public static void main(String[] args) { Integer[] array1 = {1, 2, 3, 4, 5}; Integer[] array2 = {4, 5, 6, 7, 8}; Set set1 = new HashSet<>(Arrays.asList(array1)); Set set2 = new HashSet<>(Arrays.asList(array2)); set1.retainAll(set2); Integer[] intersection = set1.toArray(new Integer[0]); System.out.println(Arrays.toString(intersection)); } }

Результат выполнения кода также будет содержать только общие элементы из двух исходных массивов: [4, 5].

Использование стандартных методов языка для поиска пересечений массивов может упростить и ускорить разработку, так как не требует написания алгоритма вручную. Однако следует учесть, что для выполнения операций над массивами могут потребоваться дополнительные системные ресурсы, особенно при работе с большими массивами данных.

Поиск пересечения в неупорядоченных массивах

Метод с использованием хэш-таблицы

Один из наиболее эффективных методов поиска пересечения в неупорядоченных массивах — использование хэш-таблицы. Для этого необходимо создать хэш-таблицу, где ключами будут элементы массива, а значениями — количество их появлений в массиве. Затем можно проходить по второму массиву и для каждого элемента проверять, есть ли он в хэш-таблице. Если элемент найден, то он является общим элементом. Этот метод имеет линейную сложность O(n+m), где n и m — размеры двух массивов.

Метод с использованием сортировки

Еще одним способом поиска пересечения в неупорядоченных массивах является сортировка массивов и последующий обход двух массивов одновременно. При сортировке массивов элементы располагаются в порядке возрастания (или убывания), что позволяет эффективно находить общие элементы. При сравнении элементов двух массивов их значения сравниваются, и если они равны, то это общий элемент. Этот метод имеет сложность O(n log n + m log m), где n и m — размеры двух массивов.

Метод	Сложность
Хэш-таблица	O(n+m)
Сортировка	O(n log n + m log m)

В зависимости от конкретной задачи и доступных ресурсов можно выбрать наиболее подходящий метод поиска пересечения массивов. Важно учитывать размеры исходных массивов, сложность алгоритма и требования к скорости выполнения.

Поиск пересечения в упорядоченных массивах

Алгоритм двух указателей основан на том, что если элементы в обоих массивах упорядочены, то можно использовать два указателя, перемещая их в зависимости от значений элементов. Это позволяет эффективно находить общие элементы без необходимости проходиться по всем элементам массивов.

Алгоритм заключается в следующем:

Инициализируйте два указателя, один для первого массива (назовем его i) и второй для второго массива (назовем его j), указывающие на первые элементы массивов.
Пока указатели не дошли до конца хотя бы одного из массивов, сравнивайте элементы, на которые указывают указатели:

Если элементы равны, то это общий элемент, добавьте его в результирующий массив и переместите оба указателя на следующие элементы.
Если элемент первого массива меньше элемента второго массива, переместите указатель первого массива на следующий элемент.
Если элемент второго массива меньше элемента первого массива, переместите указатель второго массива на следующий элемент.

Таким образом, в результате работы алгоритма двух указателей мы получим массив, содержащий только общие элементы из двух упорядоченных массивов.

Важно отметить, что данный алгоритм работает только для упорядоченных массивов. Если массивы не упорядочены, то для поиска общих элементов может потребоваться использовать другие алгоритмы, такие как алгоритмы с использованием хэш-таблиц или сортировку и бинарный поиск.

Пример	Входные массивы	Результат
1	[1, 2, 3, 4, 5]	[2, 4, 5]
2	[2, 4, 6, 8, 10]	[2, 4]
3	[1, 3, 5, 7, 9]	[]

Таким образом, алгоритм двух указателей позволяет эффективно находить общие элементы в упорядоченных массивах и может быть использован в различных задачах, где требуется поиск пересечения массивов.